Picturing structure constants

As mentioned before, in the Chevalley basis the structure constants \(K_{ij}\) obey
\[
[e_{\alpha_i}, e_{\alpha_j}] = K_{ij}\,e_{\alpha_i+\alpha_j}
\] or vanish. I.e., the commutator of the generators \(e_{\alpha_i}\) and \(e_{\alpha_j}\) either is zero or collinear to one specific generator (and not a linear combination of two or more generators) with constant of proportionality \(K_{ij}\).

With the help of LieTools I created plots of \(K_{ij}\) for some classical and the five exceptional Lie algebras. The following figures show the \(K_{ij}\)'s as a function of root numbers \(i\) and \(j\) corresponding to the (non-zero) roots \(\alpha_i\) and \(\alpha_j\).

Fig. 1: Structure constants for Lie algebra A looping thru rank 1 to 13.

In the case of An (\(n=1,2,3,\ldots\)) the structure constants \(K_{ij}\) are \(-1\), \(0\) or \(+1\). Since \(K_{ij} = -K_{ji}\), the figures are anti-symmetric with respect to the main diagonal. In addition, for root numbers close to zero (and larger ranks) there appears to be an approximate symmetry with respect to the horizontal and vertical lines.

Fig. 2: Structure constants for Lie algebra B looping thru rank 2 to 13.

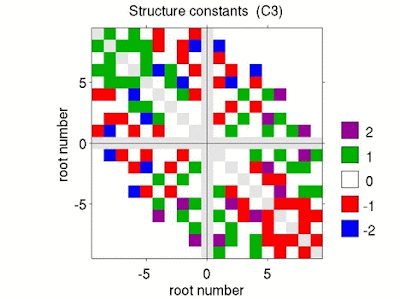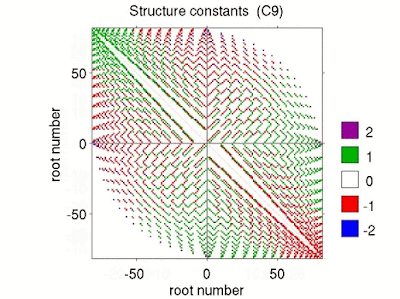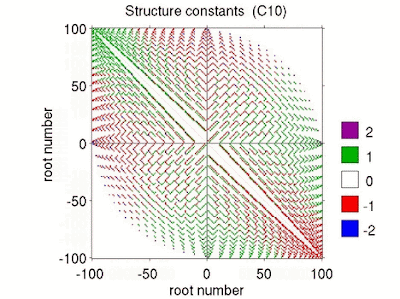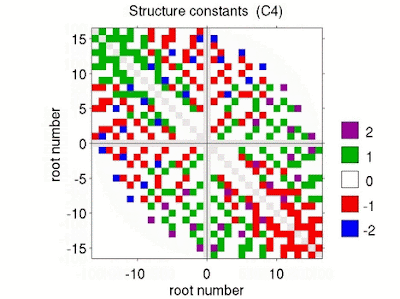Fig. 3: Structure constants for Lie algebra C looping thru rank 3 to 13.

The corresponding plots for the Lie algebras Bn (\(n\ge 2\)) and Cn (\(n\ge 3\)) (Figs. 2 and 3) show structure constants ranging from\(-2\) to \(+2\). It appears that values \(\pm 2\) occur solely within a square region centered at the origin with edge length \(\approx 1.5\cdot i_{max}\) and a circle centered at the origin with radius \(i_{max}\) for the algebras B and C, respectively. Here, \(i_{max}\) denotes the maximum root number (half of the total number of non-zero roots). 

Fig. 4: Structure constants for Lie algebra D looping thru rank 4 to 13.

The color-coded structure constants for the exceptional Lie algebras E6, E7, E8, F4 and G2 are shown in the remaining three figures with fig. 5 looping thru E6, E7 and E8. Surprisingly (to me), the plots for the exceptional algebras lack the somewhat regular patterns which are found Figs. 1 - 4.

Fig. 5: Structure constants for Lie algebra E looping thru rank 6 to 8.

Fig. 6: Structure constants for Lie algebra F (rank4)

Fig. 7: Structure constants for Lie algebra G (rank 2)

The Lie algebra G2 is the only one with structure constants varying between \(-3\) and \(+3\).