Real representations of the Lie algebra $\mathfrak{so}(3)$

Recently I wondered about the real (irreducible) representations of the Lie group SO(3) and its Lie algebra $\mathfrak{so}(3)$. It is well known, that the representations of SO(3) are odd-dimensional, there are no (irreducible) representations of SO(3) in even dimensions.

Usually, in textbooks the authors quickly move from SO(3) to the covering group SU(2) and derive the (complex) representations of the corresponding Lie algebra $\mathfrak{su}(2)$ using quantum mechanical angular momentum algebra and ladder operators.

There appears to be surprisingly little in the published literature on real-valued representations of $\mathfrak{so}(3)$. How do the real-valued representations look like? A google search lead me to

V. M. Gordienko
Matrix entries of real representations of the group O(3) and SO(3)
Siberian Mathematical Journal (2002), 43(1):36-46
DOI: 10.1023/A:1013816403253

who describes their construction; but see also

G. Itzkowitz, S. Rothman and H. Strassberg
A note on the real representation of SU(2,C)
Journal of Pure and Applied Algebra (1990), 69:285-294
DOI: 10.1016/0022-4049(91)90023-U

If I understand correctly, there is no ladder operator approach for real representations. Rather, Gordienko constructs real representations using homogeneous polynomials $P^{(N)}(x,y)$ in $x$ and $y$ with $x,y \in \mathbb{C}$. I.e.
$$\begin{align} P^{(1)}(x,y) =& a_1 x^2 + a_2 x y + a_3 y^2 \\ P^{(2)}(x,y) =& a_1 x^4 + a_2 x^3 y + a_3 x^2 y^2 + a_4 x y^3 + a_5 y^4 \notag\\ & \ldots \notag\\ P^{(N)}(x,y) =& a_1 x^{2N} + a_2 x^{2N-1} y + a_3 x^{2N-2} y^2 \notag\\ &+ \ldots + a_{N+1} x^{N} y^{N} + \ldots + a_{2N} x y^{2N-1} + a_{2N+1} y^{2N} \notag\\ \end{align}$$ Gordienko chooses the following basis in the vector space of polynomials $P^{(N)}(x,y)$
$$\begin{align} e^{(N)}_n(x,y) =& i^{N+1}\sqrt{\frac{(2N+1)!}{2(N-n)!(N+n)!}} \\ &\times(x^{N-n}y^{N+n} - (-1)^{-n}x^{N+n}y^{N-n}) \quad \mathrm{if}\; n \le -1 \notag\\ e^{(N)}_{n=0}(x,y) =&  i^{N} \frac{\sqrt{(2N+1)!}}{N!} x^N y^N \quad \mathrm{if}\; n = 0 \notag\\ e^{(N)}_n(x,y) =& -i^{N}\sqrt{\frac{(2N+1)!}{2(N+n)!(N-n)!}} \notag\\ & \times(x^{N+n}y^{N-n} + (-1)^{n}x^{N-n}y^{N+n}) \quad \mathrm{if}\; n \ge 1 \notag \end{align}$$ with $n = -N,\ldots,N$. Now let's take a generic rotation matrix from the group SU(2), parametrized by the three real numbers $\alpha$, $\beta$ and $\gamma$ and we write with $\delta\equiv\sqrt{1-\alpha^2-\beta^2-\gamma^2}$
$$M =  \begin{pmatrix} \delta - i\gamma & \beta  -i\alpha\\ -\beta - i\alpha &\delta + i\gamma \end{pmatrix} \equiv \begin{pmatrix} A^* & B^*\\ -B & A \end{pmatrix}$$ and apply it on the 2-dimensional complex vector (x,y), i.e.
$$(x',y') \equiv (x,y)  \begin{pmatrix} A^* & B^*\\ -B & A \end{pmatrix}=(A^*x-By, B^*x+Ay)$$ For the "rotated" basis $e^{(N)}_n(x',y')$ we obtain
$$\begin{align} e^{(N)}_n(x',y') =& e^{(N)}_n(A^*x-By, B^*x+Ay) \\ =& \sum_{m=-N}^{+N} T^{(N)}_{n,m}(A,B) \; e^{(N)}_m(x,y)\notag \end{align}$$ The $(2N+1)\times(2N+1)$ matrix $T^{(N)}_{m,n}(A,B)$ is the $(2N+1)$-dimensional representation matrix of SO(3) we're looking for.

Why is $T^{(N)}_{m,n}(A,B)$ real-valued? Turns out, the basis vectors $e^{(N)}_n(x,y)$ are constructed in such a way that
$$e^{(N)}_m(x,y) = (e^{(N)}_m(-y,x))^*$$ holds, where $x^*$ denotes the complex conjugate of $x$. Gordienko shows that for basis vectors with this property the entries of the representation matrices $T^{(N)}_{n,m}(A,B)$ are indeed real. Specifically,
$$\begin{align} e^{(N)}_m(x',y') =& e^{(N)}_m(A^*x-By, B^*x+Ay) \\ =&  (e^{(N)}_m(-B^*x-Ay,A^*x-By))^* \notag\\ =&  (e^{(N)}_m(B^*(-x)+A(-y),A^*x-By))^* \notag\\ =&  (e^{(N)}_m(-y',x'))^* \notag\\ =&  (\sum_{n=-N}^N T^{(N)}_{m,n}(A,B)\;e^{(N)}_n(-y,x))^* \notag\\ =&  \sum_{n=-N}^N (T^{(N)}_{m,n}(A,B))^*\;(e^{(N)}_n(-y,x))^* \notag\\ =&  \sum_{n=-N}^N (T^{(N)}_{m,n}(A,B))^*\;e^{(N)}_n(x,y) \notag \end{align}$$ Thus, $T^{(N)}_{m,n}(A,B) = (T^{(N)}_{m,n}(A,B))^*$ since the $e^{(N)}_n(x,y)$ are linear independent; in other words, the matrix $T^{(N)}_{m,n}(A,B)$ is real.

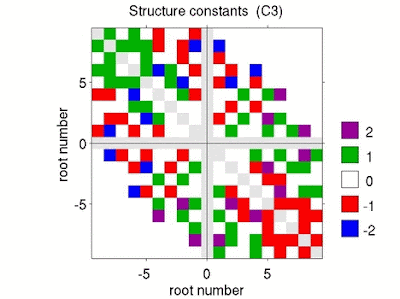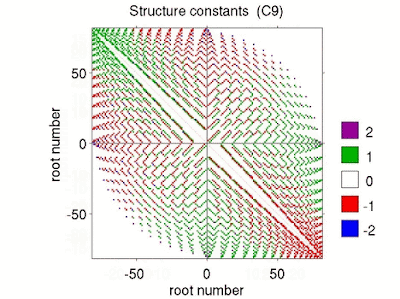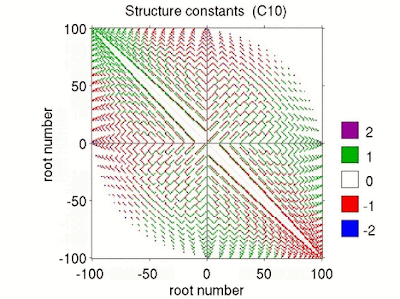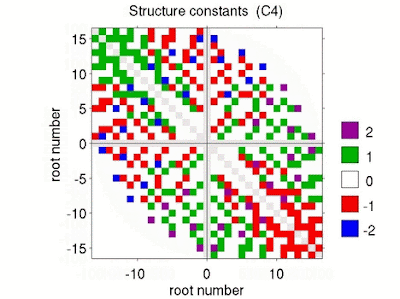
representationofso3.m a is a rough-and-ready MATLAB programme (included in LieTools), which outputs numerical approximations of the n-dimensional representations of $\mathfrak{so}(3)$ (for n below about 90) using the method described above. For dimensions 3, 5 and 7 the output of representationofso3.m yields the following matrices. The 3-dimensional representation is familiar
$$\begin{equation} t_1 = \begin{pmatrix} 0 & 1 & 0 \\ -1 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}\\ t_2 = \begin{pmatrix} 0 & 0 & -1 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \end{pmatrix}\\ t_3 = \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & -1 & 0 \end{pmatrix} \end{equation}$$ the 5-dimensional representation is $$\begin{equation} t_1 = \begin{pmatrix} 0 & 0 & 0 & -1 & 0 \\ 0 & 0 & \sqrt{3} & 0 & 1 \\ 0 & -\sqrt{3} & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 & 0 \end{pmatrix}\\ t_2 = \begin{pmatrix} 0 & 0 & 0 & 0 & -2 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 & 0 \\ 2 & 0 & 0 & 0 & 0 \end{pmatrix}\\ t_3 = \begin{pmatrix} 0 & -1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & -\sqrt{3} & 0 \\ 0 & 0 & \sqrt{3} & 0 & -1 \\ 0 & 0 & 0 & 1 & 0 \end{pmatrix} \end{equation}$$ and the 7-dimensional representation turns out to be
$$\begin{equation} t_1 = \begin{pmatrix} 0 & 0 & 0 & 0 & 0 & -\sqrt{3/2} & 0 \\ 0 & 0 & 0 & 0 & \sqrt{5/2} & 0 & \sqrt{3/2} \\ 0 & 0 & 0 & \sqrt{6} & 0 & -\sqrt{5/2} & 0 \\ 0 & 0 & -\sqrt{6} & 0 & 0 & 0 & 0 \\ 0 & -\sqrt{5/2} & 0 & 0 & 0 & 0 & 0 \\ \sqrt{3/2} & 0 & \sqrt{5/2} & 0 & 0 & 0 & 0 \\ 0 & -\sqrt{3/2} & 0 & 0 & 0 & 0 & 0 \end{pmatrix}\\ t_2 = \begin{pmatrix} 0 & 0 & 0 & 0 & 0 & 0 & -3 \\ 0 & 0 & 0 & 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 0 & -1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & -2 & 0 & 0 & 0 & 0 & 0 \\ 3 & 0 & 0 & 0 & 0 & 0 & 0 \end{pmatrix}\\ t_3 = \begin{pmatrix} 0 & -\sqrt{3/2} & 0 & 0 & 0 & 0 & 0 \\ \sqrt{3/2} & 0 & -\sqrt{5/2} & 0 & 0 & 0 & 0 \\ 0 & \sqrt{5/2} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & \sqrt{6} & 0 & 0 \\ 0 & 0 & 0 & -\sqrt{6} & 0 & -\sqrt{5/2} & 0 \\ 0 & 0 & 0 & 0 & \sqrt{5/2} & 0 & -\sqrt{3/2} \\ 0 & 0 & 0 & 0 & 0 & \sqrt{3/2} & 0 \end{pmatrix} \end{equation}$$ The zero entries in the off-diagonals look somewhat strange, but the matrices are definitely real, skew-symmetric and obey the $\mathfrak{so}(3)$ commutation relations
$$[t_1,t_2] = t_3\\ [t_2,t_3] = t_1\\ [t_3,t_1] = t_2$$

Picturing structure constants

As mentioned before, in the Chevalley basis the structure constants $K_{ij}$ obey
$$[e_{\alpha_i}, e_{\alpha_j}] = K_{ij}\,e_{\alpha_i+\alpha_j}$$ or vanish. I.e., the commutator of the generators $e_{\alpha_i}$ and $e_{\alpha_j}$ either is zero or collinear to one specific generator (and not a linear combination of two or more generators) with constant of proportionality $K_{ij}$.

With the help of LieTools I created plots of $K_{ij}$ for some classical and the five exceptional Lie algebras. The following figures show the $K_{ij}$'s as a function of root numbers $i$ and $j$ corresponding to the (non-zero) roots $\alpha_i$ and $\alpha_j$.

Fig. 1: Structure constants for Lie algebra A looping thru rank 1 to 13.

In the case of An ($n=1,2,3,\ldots$) the structure constants $K_{ij}$ are $-1$, $0$ or $+1$. Since $K_{ij} = -K_{ji}$, the figures are anti-symmetric with respect to the main diagonal. In addition, for root numbers close to zero (and larger ranks) there appears to be an approximate symmetry with respect to the horizontal and vertical lines.

Fig. 2: Structure constants for Lie algebra B looping thru rank 2 to 13.

Fig. 3: Structure constants for Lie algebra C looping thru rank 3 to 13.

The corresponding plots for the Lie algebras Bn ($n\ge 2$) and Cn ($n\ge 3$) (Figs. 2 and 3) show structure constants ranging from$-2$ to $+2$. It appears that values $\pm 2$ occur solely within a square region centered at the origin with edge length $\approx 1.5\cdot i_{max}$ and a circle centered at the origin with radius $i_{max}$ for the algebras B and C, respectively. Here, $i_{max}$ denotes the maximum root number (half of the total number of non-zero roots). 

Fig. 4: Structure constants for Lie algebra D looping thru rank 4 to 13.

The color-coded structure constants for the exceptional Lie algebras E6, E7, E8, F4 and G2 are shown in the remaining three figures with fig. 5 looping thru E6, E7 and E8. Surprisingly (to me), the plots for the exceptional algebras lack the somewhat regular patterns which are found Figs. 1 - 4.

Fig. 5: Structure constants for Lie algebra E looping thru rank 6 to 8.

Fig. 6: Structure constants for Lie algebra F (rank4)

Fig. 7: Structure constants for Lie algebra G (rank 2)

The Lie algebra G2 is the only one with structure constants varying between $-3$ and $+3$.

Structure constants

Previously on Visual Lie Theory it was mentioned, that the commutator of two basis elements of a Lie algebra $\cal{L}$ is again an element of $\cal{L}$. I.e., it can be written as a linear combination of the basis vectors $t_k, k=1,\ldots,d$; i.e.,
$$[t_i, t_j] = \sum_{k=1}^d f^k_{ij}\,t_k$$ From the literature I learn, that the parameters $f^k_{ij}$ ("structure constants") (almost?) completely describe the Lie algebra $\cal{L}$.

What's interesting about the structure constants is, that once the $f^k_{ij}$ are known, one immediately can write down a $d$-dimensional matrix representation of $\cal{L}$, the adjoint representation. Concretely, the adjoint representation of $t_i$, the $i$-th generator, is given by
$$(T_i)_{k,j}  =  f^k_{ij}$$ where $j = 1,\ldots,d$ and $k = 1,\ldots,d$ denote the row and column index of the matrix $T_i$.

Clearly,  the structure constants depend on the chosen basis vectors $t_k, k=1,\ldots,d$. Viewed from another basis $$t_k \rightarrow \tilde{t}_k \equiv \sum_{l=1}^d a^l_k\,t_l$$ the structure constants will change as well;
$$[\tilde{t}_i, \tilde{t}_j] = \sum_{k=1}^d \tilde{f}^k_{ij}\,\tilde{t}_k$$ It turns out, that there is a particular basis, known as the Chevalley basis, in which the $f^k_{ij}$ are integers and assume only values between $-3$ and $+3$; in addition, the sum in $$[t_i, t_j] = \sum_{k=1}^d f^k_{ij}\,t_k$$ contains at most one non-zero element.

In general, the generators $t_i, i=1,\ldots,d$ can be divided in $d-r$ generators $e_\alpha$ corresponding to non-zero roots and $r$ generators $h_\alpha$ corresponding to zero roots; $d$ being the dimension and $r$ being the rank of $\cal{L}$. Here, the label $i$ of the generator $t_i$ is replaced by the root $\alpha$, which we may regard as a $r$-dimensional index of $e_\alpha$ and $h_\alpha$. For the generators $e_\alpha$ we find
$$[e_{\alpha_i}, e_{\alpha_j}] = K_{ij}\,e_{\alpha_i+\alpha_j}$$ where $K_{ij}$ is non-zero if the sum $\alpha_i+\alpha_j$ is a non-zero root. If $\alpha_i+\alpha_j$ is not a root, the commutator vanishes ($K_{ij}=0$). If $\alpha_i+\alpha_j$ is a zero-root (i.e. $\alpha_j = -\alpha_i$) the commutator is
$$[e_{\alpha_i}, e_{-\alpha_i}] = h_{\alpha_i}$$ where $h_{\alpha_i}$ is an element of the Cartan subalgebra. All generators contained within the Cartan subalgebra commute, i.e.
$$[h_{\alpha_i}, h_{\alpha_j}] = 0$$ . Furthermore,
$$[h_{\alpha_i}, e_{\alpha_j}] = N_{ij}\,e_{\alpha_j}$$ with $N_{ij}$ being the entries of the Cartan matrix.

Since all information on $\cal{L}$ supposedly is encoded in the $f^k_{ij}$, naively I had expected that there existed tables of  $f^k_{ij}$ (or $K_{ij}$) for all (classical and exceptional) Lie algebras. My web search, however, turned up surprisingly little - perhaps I looked at all the wrong places.

So how does one (or a computer) then actually calculate the $f^k_{ij}$? The following two papers I found most useful for finding an answer :

1. V. K. Agrawala and Johan G. Belinfante: Weight diagrams for lie group representations: A computer implementation of Freudenthal's algorithm in ALGOL and FORTRAN, BIT (1969) 9(4):301-314. doi: 10.1007/BF01935862
2. R.B Howlett, L.J Rylands, D.E Taylor: Matrix Generators for Exceptional Groups of Lie Type, Journal of Symbolic Computation, volume 31, issue 4, April 2001, pages 429-445, doi: 10.1006/jsco.2000.0431

Based on algorithms and source code contained therein I wrote some MATLAB programs (the only computer language I speak somewhat fluently) for the calculation of the coefficients $K_{ij}$; these tools ("LieTools") are available for download here. (At this point Octave is not (yet) supported due to Octave's missing implementation of nested functions.)

Fig. 1: Structure constants $K_{ij}$ for the Lie algebra F4 (52 dimensions, i.e. 52-4=48 non-zero roots)

As an example figure 1 shows a graphical representation of (what "LieTools" thinks are) the coefficients $K_{ij}$ for the exceptional Lie algebra F4. In the Chevalley basis the $K_{ij}$ assume one of five possible value, $-2,-1,0,+1,+2$, here plotted in 5 different colours. (You've probably noticed that I used part of this figure for the blog header.)