Picturing structure constants

As mentioned before, in the Chevalley basis the structure constants $K_{ij}$ obey
$$[e_{\alpha_i}, e_{\alpha_j}] = K_{ij}\,e_{\alpha_i+\alpha_j}$$ or vanish. I.e., the commutator of the generators $e_{\alpha_i}$ and $e_{\alpha_j}$ either is zero or collinear to one specific generator (and not a linear combination of two or more generators) with constant of proportionality $K_{ij}$.

With the help of LieTools I created plots of $K_{ij}$ for some classical and the five exceptional Lie algebras. The following figures show the $K_{ij}$'s as a function of root numbers $i$ and $j$ corresponding to the (non-zero) roots $\alpha_i$ and $\alpha_j$.

Fig. 1: Structure constants for Lie algebra A looping thru rank 1 to 13.

In the case of An ($n=1,2,3,\ldots$) the structure constants $K_{ij}$ are $-1$, $0$ or $+1$. Since $K_{ij} = -K_{ji}$, the figures are anti-symmetric with respect to the main diagonal. In addition, for root numbers close to zero (and larger ranks) there appears to be an approximate symmetry with respect to the horizontal and vertical lines.

Fig. 2: Structure constants for Lie algebra B looping thru rank 2 to 13.

Fig. 3: Structure constants for Lie algebra C looping thru rank 3 to 13.

The corresponding plots for the Lie algebras Bn ($n\ge 2$) and Cn ($n\ge 3$) (Figs. 2 and 3) show structure constants ranging from$-2$ to $+2$. It appears that values $\pm 2$ occur solely within a square region centered at the origin with edge length $\approx 1.5\cdot i_{max}$ and a circle centered at the origin with radius $i_{max}$ for the algebras B and C, respectively. Here, $i_{max}$ denotes the maximum root number (half of the total number of non-zero roots). 

Fig. 4: Structure constants for Lie algebra D looping thru rank 4 to 13.

The color-coded structure constants for the exceptional Lie algebras E6, E7, E8, F4 and G2 are shown in the remaining three figures with fig. 5 looping thru E6, E7 and E8. Surprisingly (to me), the plots for the exceptional algebras lack the somewhat regular patterns which are found Figs. 1 - 4.

Fig. 5: Structure constants for Lie algebra E looping thru rank 6 to 8.

Fig. 6: Structure constants for Lie algebra F (rank4)

Fig. 7: Structure constants for Lie algebra G (rank 2)

The Lie algebra G2 is the only one with structure constants varying between $-3$ and $+3$.

Structure constants

Previously on Visual Lie Theory it was mentioned, that the commutator of two basis elements of a Lie algebra $\cal{L}$ is again an element of $\cal{L}$. I.e., it can be written as a linear combination of the basis vectors $t_k, k=1,\ldots,d$; i.e.,
$$[t_i, t_j] = \sum_{k=1}^d f^k_{ij}\,t_k$$ From the literature I learn, that the parameters $f^k_{ij}$ ("structure constants") (almost?) completely describe the Lie algebra $\cal{L}$.

What's interesting about the structure constants is, that once the $f^k_{ij}$ are known, one immediately can write down a $d$-dimensional matrix representation of $\cal{L}$, the adjoint representation. Concretely, the adjoint representation of $t_i$, the $i$-th generator, is given by
$$(T_i)_{k,j}  =  f^k_{ij}$$ where $j = 1,\ldots,d$ and $k = 1,\ldots,d$ denote the row and column index of the matrix $T_i$.

Clearly,  the structure constants depend on the chosen basis vectors $t_k, k=1,\ldots,d$. Viewed from another basis $$t_k \rightarrow \tilde{t}_k \equiv \sum_{l=1}^d a^l_k\,t_l$$ the structure constants will change as well;
$$[\tilde{t}_i, \tilde{t}_j] = \sum_{k=1}^d \tilde{f}^k_{ij}\,\tilde{t}_k$$ It turns out, that there is a particular basis, known as the Chevalley basis, in which the $f^k_{ij}$ are integers and assume only values between $-3$ and $+3$; in addition, the sum in $$[t_i, t_j] = \sum_{k=1}^d f^k_{ij}\,t_k$$ contains at most one non-zero element.

In general, the generators $t_i, i=1,\ldots,d$ can be divided in $d-r$ generators $e_\alpha$ corresponding to non-zero roots and $r$ generators $h_\alpha$ corresponding to zero roots; $d$ being the dimension and $r$ being the rank of $\cal{L}$. Here, the label $i$ of the generator $t_i$ is replaced by the root $\alpha$, which we may regard as a $r$-dimensional index of $e_\alpha$ and $h_\alpha$. For the generators $e_\alpha$ we find
$$[e_{\alpha_i}, e_{\alpha_j}] = K_{ij}\,e_{\alpha_i+\alpha_j}$$ where $K_{ij}$ is non-zero if the sum $\alpha_i+\alpha_j$ is a non-zero root. If $\alpha_i+\alpha_j$ is not a root, the commutator vanishes ($K_{ij}=0$). If $\alpha_i+\alpha_j$ is a zero-root (i.e. $\alpha_j = -\alpha_i$) the commutator is
$$[e_{\alpha_i}, e_{-\alpha_i}] = h_{\alpha_i}$$ where $h_{\alpha_i}$ is an element of the Cartan subalgebra. All generators contained within the Cartan subalgebra commute, i.e.
$$[h_{\alpha_i}, h_{\alpha_j}] = 0$$ . Furthermore,
$$[h_{\alpha_i}, e_{\alpha_j}] = N_{ij}\,e_{\alpha_j}$$ with $N_{ij}$ being the entries of the Cartan matrix.

Since all information on $\cal{L}$ supposedly is encoded in the $f^k_{ij}$, naively I had expected that there existed tables of  $f^k_{ij}$ (or $K_{ij}$) for all (classical and exceptional) Lie algebras. My web search, however, turned up surprisingly little - perhaps I looked at all the wrong places.

So how does one (or a computer) then actually calculate the $f^k_{ij}$? The following two papers I found most useful for finding an answer :

1. V. K. Agrawala and Johan G. Belinfante: Weight diagrams for lie group representations: A computer implementation of Freudenthal's algorithm in ALGOL and FORTRAN, BIT (1969) 9(4):301-314. doi: 10.1007/BF01935862
2. R.B Howlett, L.J Rylands, D.E Taylor: Matrix Generators for Exceptional Groups of Lie Type, Journal of Symbolic Computation, volume 31, issue 4, April 2001, pages 429-445, doi: 10.1006/jsco.2000.0431

Based on algorithms and source code contained therein I wrote some MATLAB programs (the only computer language I speak somewhat fluently) for the calculation of the coefficients $K_{ij}$; these tools ("LieTools") are available for download here. (At this point Octave is not (yet) supported due to Octave's missing implementation of nested functions.)

Fig. 1: Structure constants $K_{ij}$ for the Lie algebra F4 (52 dimensions, i.e. 52-4=48 non-zero roots)

As an example figure 1 shows a graphical representation of (what "LieTools" thinks are) the coefficients $K_{ij}$ for the exceptional Lie algebra F4. In the Chevalley basis the $K_{ij}$ assume one of five possible value, $-2,-1,0,+1,+2$, here plotted in 5 different colours. (You've probably noticed that I used part of this figure for the blog header.)

Watching the Lie algebra $\mathfrak{su}(3)$ at work

Just as in the post on $\mathfrak{su}(2)$, we may attempt to visualize the effect of the $\mathfrak{su}(3)$ rotations

$$\begin{equation*} t_x = \frac{i}{2}\,\begin{pmatrix} 0 & -1 & 0\\ -1 & 0 & 0\\ 0 & 0 & 0 \end{pmatrix} \quad t_y = \frac{i}{2}\,\begin{pmatrix} 0  & i & 0 \\ -i & 0 & 0 \\ 0 & 0 & 0  \end{pmatrix} \quad t_z = \frac{i}{2}\,\begin{pmatrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{pmatrix}\\ u_x = \frac{i}{2}\,\begin{pmatrix} 0 & 0 & 0\\ 0 & 0 & -1\\ 0 & -1 & 0 \end{pmatrix}\quad u_y = \frac{i}{2}\,\begin{pmatrix} 0 & 0 & 0 \\ 0 & 0  & i \\ 0 & -i & 0 \end{pmatrix}\quad u_z = \frac{i}{2}\,\begin{pmatrix} 0 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{pmatrix}\\ v_x = \frac{i}{2}\,\begin{pmatrix} 0 & 0 & -1\\ 0 & 0 & 0\\ -1 & 0 & 0 \end{pmatrix}\quad v_y = \frac{i}{2}\,\begin{pmatrix} 0  & 0 & i \\ 0 & 0 & 0 \\ -i & 0 & 0  \end{pmatrix}\quad v_z = \frac{i}{2}\,\begin{pmatrix} -1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \end{pmatrix} \end{equation*}$$ As already noted $v_z = t_z+u_z$, leaving only eight linear independent generators. The resulting animation is shown in Fig. 1.

Fig. 1: The Lie algebra su(3) at work

The red, green and blue symbols mark three unit squares [(0,0), (1,0), (1,i), (0,i)], one in each of the three complex planes which constitute the three-dimensional complex space. The animations show the motion of the three squares when rotated by $T_x= \mathbb{1}+\alpha\cdot t_x$, $T_y = \mathbb{1}+\alpha\cdot t_y$, etc.; here, $\alpha$ denotes the (infinitesimal) rotation angle. Note that it requires an accumulated rotation of $4\,\pi$ for the squares to return to their original position.

When we examine the right-most three (sub-)figures of Fig. 1 it actually can be seen that $V_z$ corresponds to the combined effect of $T_z$ and $U_z$. E.g. the anti-clockwise rotation of the blue square generated by $T_z$ and its clockwise rotation generated by $U_z$ cancel out causing it to remain fixed when $V_z$ is applied.

The Lie algebra $\mathfrak{su}(3)$

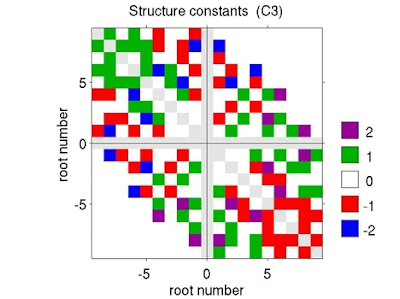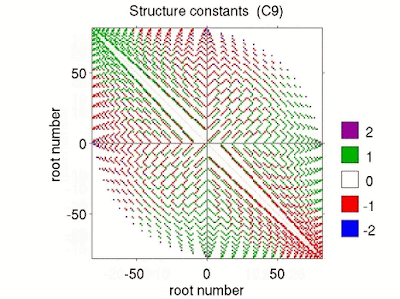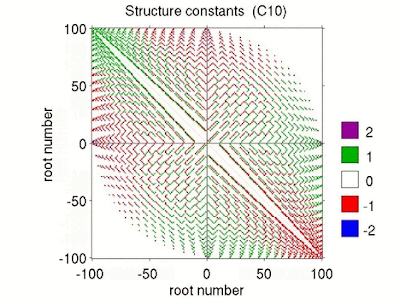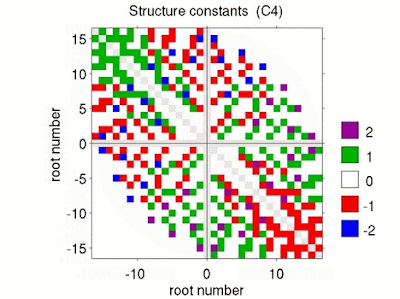
When looking at the three $\mathfrak{su}(2)$ generator matrices
$$\begin{equation} t_x = \frac{i}{2}\,\begin{pmatrix} 0 & -1 \\ -1 & 0 \end{pmatrix}\\ t_y = \frac{i}{2}\,\begin{pmatrix} 0  & i \\ -i & 0  \end{pmatrix}\\ t_z = \frac{i}{2}\,\begin{pmatrix} -1 & 0 \\0 & 1 \end{pmatrix} \label{lasu3:eq:repre1} \end{equation}$$ (see this post) one could be tempted to assume that the nine matrices
$$\begin{equation} t_x = \frac{i}{2}\,\begin{pmatrix} 0 & -1 & 0\\ -1 & 0 & 0\\ 0 & 0 & 0 \end{pmatrix}\qquad t_y = \frac{i}{2}\,\begin{pmatrix} 0  & i & 0 \\ -i & 0 & 0 \\ 0 & 0 & 0  \end{pmatrix}\\ t_z = \frac{i}{2}\,\begin{pmatrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{pmatrix}\qquad u_x = \frac{i}{2}\,\begin{pmatrix} 0 & 0 & 0\\ 0 & 0 & -1\\ 0 & -1 & 0 \end{pmatrix}\\ u_y = \frac{i}{2}\,\begin{pmatrix} 0 & 0 & 0 \\ 0 & 0  & i \\ 0 & -i & 0 \end{pmatrix}\qquad u_z = \frac{i}{2}\,\begin{pmatrix} 0 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{pmatrix}\\ v_x = \frac{i}{2}\,\begin{pmatrix} 0 & 0 & -1\\ 0 & 0 & 0\\ -1 & 0 & 0 \end{pmatrix}\qquad v_y = \frac{i}{2}\,\begin{pmatrix} 0  & 0 & i \\ 0 & 0 & 0 \\ -i & 0 & 0  \end{pmatrix}\\ v_z = \frac{i}{2}\,\begin{pmatrix} -1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \end{pmatrix} \label{lasu3:eq:repre2} \end{equation}$$ form a Lie algebra as well. Calculation of all 81 commutators (Lie products) yields :

	$t_x$	$t_y$	$t_z$	$u_x$	$u_y$	$u_z$	$v_x$	$v_y$	$v_z$
$t_x$	$0$	$t_z$	$-t_y$	${v_y\over 2}$	$-{v_x\over 2}$	${t_y\over 2}$	${u_y\over 2}$	$-{u_x\over 2}$	$-{t_y\over 2}$
$t_y$	$-t_z$	$0$	$t_x$	$-{v_x\over 2}$	${v_y\over 2}$	$-{t_x\over 2}$	$-{u_x\over 2}$	${u_y\over 2}$	${t_x\over 2}$
$t_z$	$t_y$	$-t_x$	$0$	$-{u_y\over 2}$	${u_x\over 2}$	$0$	${v_y\over 2}$	$-{v_x\over 2}$	$0$
$u_x$	$-{v_y\over 2}$	${v_x\over 2}$	${u_y\over 2}$	$0$	$u_z$	$-u_y$	$-{t_y\over 2}$	${t_x\over 2}$	$-{u_y\over 2}$
$u_y$	${v_x\over 2}$	$-{v_y\over 2}$	$-{u_x\over 2}$	$-u_z$	$0$	$u_x$	$-{t_x\over 2}$	${t_y\over 2}$	${u_x\over 2}$
$u_z$	$-{t_y\over 2}$	${t_x\over 2}$	$0$	$u_y$	$-u_x$	$0$	${v_y\over 2}$	$-{v_x\over 2}$	$0$
$v_x$	$-{u_y\over 2}$	${u_x\over 2}$	$-{v_y\over 2}$	${t_y\over 2}$	${t_x\over 2}$	$-{v_y\over 2}$	$0$	$v_z$	$-v_y$
$v_y$	${u_x\over 2}$	$-{u_y\over 2}$	${v_x\over 2}$	$-{t_x\over 2}$	$-{t_y\over 2}$	${v_x\over 2}$	$-v_z$	$0$	$v_x$
$v_z$	${t_y\over 2}$	$-{t_x\over 2}$	$0$	${u_y\over 2}$	$-{u_x\over 2}$	$0$	$v_y$	$-v_x$	$0$

(The row value is the first entry, the column value the seconds entry in the commutator $[\cdot, \cdot]$.) The yellow-colored values mark the Lie product of $t_x$, $t_y$, $t_z$ with themselves (green for $u_x$, $u_y$, $u_z$, blue for $v_x$, $v_y$, $v_z$) and suggest that this algebra includes three copies of $su(2)$.
 
Alas, the set $t_x$, $t_y$, $t_z$, $u_x$, $u_y$, $u_z$, $v_x$, $v_y$ and $v_z$ doesn't form a basis since only eight of the nine vectors are linear independent. E.g., we find $v_z = t_z + u_z$ and we could choose the eight elements $t_x$, $t_y$, $t_z$, $u_x$, $u_y$, $u_z$, $v_x$, $v_y$. Of course, instead of $v_z$ we could just as well disregard $t_z$ or $u_z$. Either way, the multiplication table loses its nice symmetry and, for the set $t_x$, $t_y$, $t_z$, $u_x$, $u_y$, $u_z$, $v_x$, $v_y$, looks like this

	$t_x$	$t_y$	$t_z$	$u_x$	$u_y$	$u_z$	$v_x$	$v_y$
$t_x$	$0$	$t_z$	$-t_y$	${v_y\over 2}$	$-{v_x\over 2}$	${t_y\over 2}$	${u_y\over 2}$	$-{u_x\over 2}$
$t_y$	$-t_z$	$0$	$t_x$	$-{v_x\over 2}$	${v_y\over 2}$	$-{t_x\over 2}$	$-{u_x\over 2}$	${u_y\over 2}$
$t_z$	$t_y$	$-t_x$	$0$	$-{u_y\over 2}$	${u_x\over 2}$	$0$	${v_y\over 2}$	$-{v_x\over 2}$
$u_x$	$-{v_y\over 2}$	${v_x\over 2}$	${u_y\over 2}$	$0$	$u_z$	$-u_y$	$-{t_y\over 2}$	${t_x\over 2}$
$u_y$	${v_x\over 2}$	$-{v_y\over 2}$	$-{u_x\over 2}$	$-u_z$	$0$	$u_x$	$-{t_x\over 2}$	${t_y\over 2}$
$u_z$	$-{t_y\over 2}$	${t_x\over 2}$	$0$	$u_y$	$-u_x$	$0$	${v_y\over 2}$	$-{v_x\over 2}$
$v_x$	$-{u_y\over 2}$	${u_x\over 2}$	$-{v_y\over 2}$	${t_y\over 2}$	${t_x\over 2}$	$-{v_y\over 2}$	$0$	$t_z+u_z$
$v_y$	${u_x\over 2}$	$-{u_y\over 2}$	${v_x\over 2}$	$-{t_x\over 2}$	$-{t_y\over 2}$	${v_x\over 2}$	$-(t_z+u_z)$	$0$

In order to show that $t_x$, $t_y$, $t_z$, $u_x$, $u_y$, $u_z$, $v_x$, $v_y$ with the Lie multiplication table shown above is indeed a Lie algebra, it needs to be checked that
$$\begin{equation*}  [a, b] = -[b, a] \\  [a, [b, c]] + [b, [c, a]] + [c, [a, b]] = 0 \end{equation*}$$ The first equation (anti-symmetry) is valid since the entries in the table form an anti-symmetric matrix. The second (Jacobi identity) needs to be checked for all $8\cdot 8\cdot 8 = 512$ possibilities, which did my computer for me. The Lie algebra of the eight vectors $t_x$, $t_y$, $t_z$, $u_x$, $u_y$, $u_z$, $v_x$, $v_y$ with the multiplication table above form the Lie algebra $\mathfrak{su}(3)$.

The Lie algebra $\mathfrak{su}(2)$

Previously, I noted that the three generator matrices
$$t_x = \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & -1 & 0 \end{pmatrix}\\ t_y = \begin{pmatrix} 0 & 0 & 1 \\0 & 0 & 0 \\ -1 & 0 & 0 \end{pmatrix}\\ t_z = \begin{pmatrix} 0 & 1 & 0 \\ -1 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}$$ obey the commutation relations
$$\begin{equation}  [t_x, t_y ] = t_z \\  [t_y, t_z ] = t_x \\  [t_z, t_x ] = t_y \label{lasu2:eq:comrel1} \end{equation}$$ It turns out that the matrices $t_x$, $t_y$ and $t_z$ may appear in a very much different form and still follow the same set of rules $\eqref{lasu2:eq:comrel1}$. E.g. the three complex-valued matrices
$$\begin{equation} t_x = \frac{i}{2}\,\begin{pmatrix} 0 & -1 \\ -1 & 0 \end{pmatrix}\\ t_y = \frac{i}{2}\,\begin{pmatrix} 0  & i \\ -i & 0  \end{pmatrix}\\ t_z = \frac{i}{2}\,\begin{pmatrix} -1 & 0 \\0 & 1 \end{pmatrix} \label{lasu2:eq:repre2} \end{equation}$$ also fulfil $\eqref{lasu2:eq:comrel1}$. These matrices generate three "sort-of-rotations" in a two-dimensional space with complex coordinates. Visualizing (in three dimensions) points moving in two-dimensional complex space (four dimensional space with real coordinates) is too difficult for me. Here is my best-effort result:

The red crosses and blue circles mark two unit squares [(0,0), (1,0), (1,i), (0,i)], one in each of the two complex planes which constitute the two-dimensional complex space. The animations show the motion of the two squares when rotated by $\mathbb{1}+\alpha\cdot t_x$ (bottom left), $\mathbb{1}+\alpha\cdot t_y$ (bottom right) and $\mathbb{1}+\alpha\cdot t_z$ (top left); $\alpha$ denotes the (infinitesimal) rotation angle. Note that it requires an accumulated rotation of $4\,\pi$ for the squares to return to their original position.

The Lie algebra described by the relations $\eqref{lasu2:eq:comrel1}$ is known as $\mathfrak{su}(2)$ - by physicists, mathematicians call it $A_1$.

From Lie groups to Lie algebras

Previously we have seen that infinitesimal rotation in three dimensions are generated by the matrices $t_x$, $t_y$ and $t_z$ which obey the commutation relations
$$\begin{equation}  [t_x, t_y ] = t_z \\  [t_y, t_z ] = t_x \\  [t_z, t_x ] = t_y \label{flg:eq:comrel1} \end{equation}$$ It turns out that $t_x$, $t_y$ and $t_z$ form the basis of a three-dimensional vector space $\cal{L}$. The commutation relations $\eqref{flg:eq:comrel1}$ imply however, that $\cal{L}$ is more than an ordinary vector space. It has additional structure, viz. a "multiplication" $[\cdot,\cdot]$ which maps two elements of $\cal{L}$ into an element of $\cal{L}$. Formally, we write
$$[a, b] = c$$ with $a$, $b$ and $c \in \cal{L}$. The "multiplication" $[\cdot,\cdot]$ is anticommutative
$$[a,b] = -[b,a]$$ and it obeys the Jacobi identity
$$[a, [b, c]] + [b, [c, a]] + [c, [a, b]] = 0$$ If a vector space is equipped with this type of "multiplication", it is called a Lie algebra.

If I understand correctly, we can already learn a lot about the Lie group $L$ if we narrow our view to these infinitesimal rotations, i.e. the local neighborhood of $L$'s unit element and study the Lie algebra $\cal{L}$ spanned by the generators $t_i$, rather that the Lie group $L$.

Restricting our investigation to the vicinity of $L$'s unit element is not a serious limitation, since any element $g$ of the Lie group $L$ can be turned into the unit element simply by multiplying all elements of $L$ with $g^{-1}$, the inverse element of $g$.

Infinitesimal rotations

This animated GIF

was created by repeatedly rotating the vertex points $(x,y,z)$ through a small angle $\alpha$ around the x-axis into the point $(x',y',z')$,
$$\begin{pmatrix} x\\ y\\ z \end{pmatrix} \rightarrow \begin{pmatrix}x'\\ y'\\ z' \end{pmatrix} = R_x(\alpha) \cdot \begin{pmatrix} x\\ y\\ z \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos\alpha & \sin\alpha \\ 0 & -\sin\alpha & \cos\alpha \end{pmatrix} \cdot \begin{pmatrix} x\\ y\\ z \end{pmatrix}$$
If $\alpha \ll 1$ we may write
$$\begin{pmatrix} x'\\ y'\\ z' \end{pmatrix} \approx \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & \alpha \\ 0 & -\alpha & 1 \end{pmatrix} \cdot \begin{pmatrix} x\\ y\\ z \end{pmatrix} = \left(\mathbb{1} + \alpha\cdot t_x\right)\cdot \begin{pmatrix} x\\ y\\ z \end{pmatrix}$$
where the matrices $\mathbb{1}$ and $t_x$ are defined as
$$\mathbb{1} \equiv \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \\ t_x \equiv \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & -1 & 0 \end{pmatrix}$$
In a sense, the matrix $t_x$ "generates" a rotation about the x-axis. Likewise, the (generator) matrices for rotations about the y- and z-axis ("y-rotation" and "z-rotation") are
$$t_y \equiv \begin{pmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ -1 & 0 & 0 \end{pmatrix}\\ t_z \equiv \begin{pmatrix} 0 & 1 & 0 \\ -1 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}$$
If I understand the Lie-terature correctly, the concept of infinitesimal rotations is one of the key ideas in the study of continuous groups.

Now one might ask how much "deviation from commutativity" is caused by two consecutive infinitesimal rotations? By "deviation from commutativity" I mean the distance between points infinitesimally rotated twice, if the order of the two infinitesimal rotations is exchanged. E.g., for infinitesimal x- and y-rotations we find
$$\left(R_x \cdot R_y - R_y \cdot R_x\right) \cdot \begin{pmatrix} x\\ y\\ z \end{pmatrix}\\ \approx \left( \left(\mathbb{1} + \alpha\cdot t_x\right)\cdot \left(\mathbb{1} + \alpha\cdot t_y\right) - \left(\mathbb{1} + \alpha\cdot t_y\right)\cdot \left(\mathbb{1} + \alpha\cdot t_x\right) \right) \cdot \begin{pmatrix} x\\ y\\ z \end{pmatrix}\\ =  \alpha^2\cdot\left(t_x \cdot t_y - t_y \cdot t_x\right) \cdot \begin{pmatrix} x\\ y\\ z \end{pmatrix}$$ which, by actually doing the matrix multiplication, is found to be
$$\alpha^2\cdot\left(t_x \cdot t_y - t_y \cdot t_x\right) \cdot \begin{pmatrix} x\\ y\\ z \end{pmatrix} =  \alpha^2\cdot t_z \cdot \begin{pmatrix} x\\ y\\ z \end{pmatrix}$$
With the notation
$$[t_x,t_y] \equiv t_x \cdot t_y - t_y \cdot t_x$$
we may write
$$\begin{equation} [t_x,t_y] = t_z \label{ir:eq:comrel1} \end{equation}$$
and likewise
$$\begin{equation}  [t_y, t_z] = t_x \\  [t_z, t_x] = t_y \label{ir:eq:comrel2} \end{equation}$$
The visual interpretation of equation $\eqref{ir:eq:comrel1}$ is illustrated here

Eight points are rotated about the x-axes, then about the y-axis. The result (blue dots) is compared with the results obtained by the same rotations, however applied in reverse order (black dots). The difference (red line) corresponds to a rotation about the z-axis. Formally, the commutator of the two infinitesimal rotations $[t_x, t_y]$ is again an infinitesimal rotation, a z-rotation generated by $t_z$.

Rotations in three dimensions

Lie groups are continuous groups. An example of a continuous group, that I manage to visualize, are rotations in three-dimensional space.

Fig. 1: An arbitrary rotation is undone by three rotations about the z-, y- and x-axes. 

Rotations form a group since:

• The result of two rotations $a$ and $b$, conducted one after the other, written formally as $a \circ b$, is again a rotation ("closure").
• A series of rotations can be grouped at will, we'll always arrive at the same result. I.e. $(a \circ b) \circ c = a \circ (b \circ c)$ ("associativity").
• Rotating an object by zero degrees is regarded a rotation as well. This operation, denoted by $e$, commutes with every other rotation $e \circ a = a \circ e$ ("identity element").
• Every rotation through an angle $\alpha$ can be undone by a rotation through $-\alpha$ ("inverse element").

Every rotation in three-dimensional space can be decomposed into a rotation about the x-axis, a rotation about the y-axis and a rotation about the z-axis (Fig. 1).

Fig.2: Three-dimensional rotations are not commutative.

Rotations in three-dimensional space are non-commutative. I.e. in general the order of the rotations does matter for the final position (Fig. 2).

Algebraically rotations are expressed in terms of 3x3 matrices.
$$R_x(\alpha) = \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos\alpha & \sin\alpha \\ 0 & -\sin\alpha & \cos\alpha \end{pmatrix} \\ R_y(\alpha) = \begin{pmatrix} \cos\alpha  & 0 & \sin\alpha \\ 0 & 1 & 0 \\ -\sin\alpha & 0 & \cos\alpha \end{pmatrix} \\ R_z(\alpha) = \begin{pmatrix} \cos\alpha  & \sin\alpha & 0 \\ -\sin\alpha & \cos\alpha & 0 \\ 0 & 0 & 1 \end{pmatrix}$$
Here, the matrix $R_x(\alpha)$ describes the rotation about the x-axis by an angle $\alpha$. E.g., the point (x,y,z) rotated by $\alpha$ about the x-axis, by $\beta$ about the y-axis and by $\gamma$ about the z-axis is given by
$$R_z(\gamma) \cdot R_y(\beta) \cdot R_x(\alpha) \cdot \begin{pmatrix} x\\ y\\ z \end{pmatrix}$$